Why Closed-Loop Kinematics Matter
Introduction
The design of bipedal robots is often guided by intuition and incremental refinement. However, with the growing complexity and performance demands of modern humanoids, leg architecture must now be approached as a rigorous engineering problem. In a recent study, I proposed a set of quantitative criteria to evaluate and compare bipedal leg designs, with particular attention to the impact of closed-loop (parallel) kinematics. This article presents the motivation behind that work and summarizes the key findings, while also revisiting the modeling principles that enable the simulation of such mechanisms.
Modeling Closed-Loop Kinematic Chains
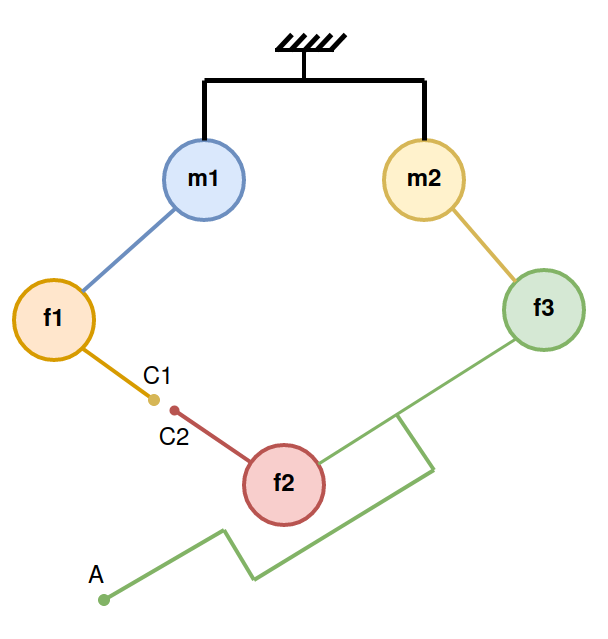
A kinematic chain becomes “closed” when multiple independent paths connect two rigid bodies, forming loops that impose nontrivial geometric constraints. To handle such systems, a numerical approach can be adopted by virtually splitting the mechanism into two open subchains and enforcing constraints between their terminal frames.
The figure illustrates this concept using a planar 5-bar mechanism:
In this model:
- Subchain 1: $m_1$, $f_1$, $C_1$
- Subchain 2: $m_2$, $f_2$, $f_3$, $C_2$
- A holonomic constraint is enforced: $C_1(q_a) = C_2(q_a)$
The loop closure constraint is expressed as:
$$ \phi(q) = C_1(q) - C_2(q) = 0 $$
where $q \in \mathbb{R}^n$ is the full configuration of the robot.
To derive the kinematics, we assume an implicit dependency $q_f = f(q_a)$. Although $f$ is not explicitly known, its Jacobian can be inferred via the implicit function theorem:
$$ \frac{\partial \phi}{\partial q_a} + \frac{\partial \phi}{\partial q_f} \cdot \frac{\partial f}{\partial q_a} = 0 $$
Solving this yields:
$$ \frac{\partial f}{\partial q_a} = - \left(\frac{\partial \phi}{\partial q_f}\right)^{-1} \cdot \frac{\partial \phi}{\partial q_a} $$
The global Jacobian relating actuator velocities to end-effector motion is then:
$$ \frac{\partial q}{\partial q_a} = \begin{bmatrix} I \ \frac{\partial f}{\partial q_a} \end{bmatrix} $$
This formulation allows evaluating Jacobians, apparent inertia, and all related dynamic quantities using standard tools like Pinocchio.
Performance Criteria for Leg Evaluation
Five core metrics were introduced to assess the quality of a leg design:
- Translational/Rotational Manipulability (TM/RM): Measures how easily the foot can translate or rotate in space given unit motor effort.
- Z-Reduction Ratio (ZRR): Quantifies the ability to support vertical loads without overloading actuators.
- Z-Axis Apparent Inertia (ZAI): Captures how much mass the robot “feels” at the foot when accelerating vertically.
- Impact Mitigation Factor (IMF): Assesses the robot’s capacity to absorb shocks dynamically.
- Compactness (V3/V2): Measures the 3D volume and sagittal footprint spanned by the leg.
These criteria were evaluated using consistent simulation tools on five robots: Digit, Talos, Kangaroo, WL16, and the Disney Biped.
 Digit |
 Disney Bipedal Robot |
 Kangaroo |
 Talos |
 WL16 |
Why Closed-Loop Kinematics Are Beneficial
Parallel or closed-loop architectures allow the redistribution of mass and actuators toward the torso. This design principle reduces distal inertia and enables:
- Lower energy consumption during fast leg swings
- Better control authority at the end-effector through multiple actuation paths
- Enhanced shock resilience due to distributed structural paths
Kangaroo, for example, integrates 11 closed loops per leg to concentrate all actuation near the hip, leading to standout performance in both manipulability and impact absorption.
Highlights from the Comparative Study
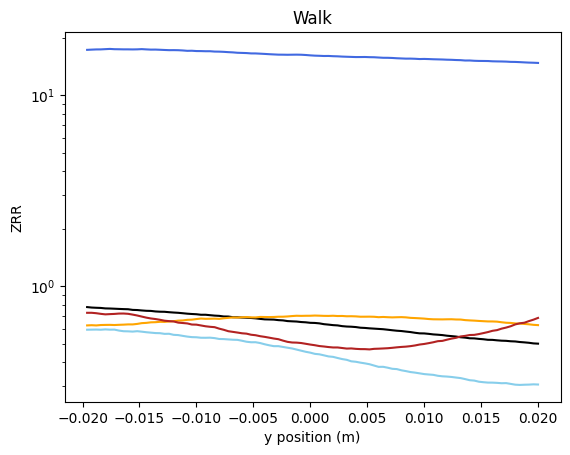 Z-Reduction Ratio over a Walking Trajectory |
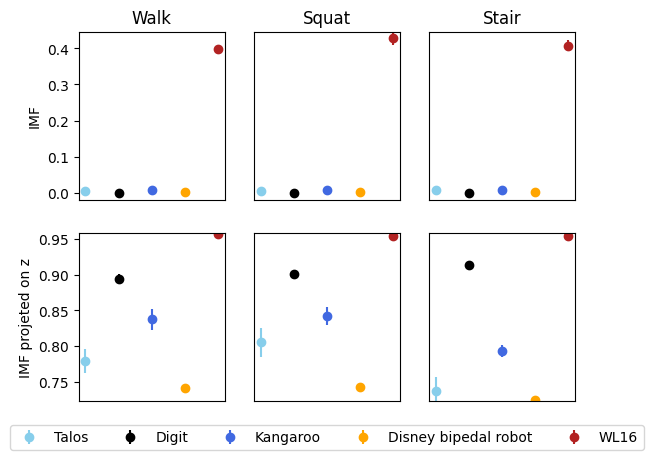 Impact Mitigation Factor |
 Legend |
- Kangaroo and WL16 excel in manipulability and shock mitigation, validating the value of closed-loop structures.
- Talos and Disney Biped suffer from high foot inertia due to distal actuators, negatively impacting energy efficiency and contact dynamics.
- Digit strikes a pragmatic balance with a hybrid serial-parallel setup that reduces foot mass without sacrificing too much compactness.
- The ZRR metric revealed the energetic cost of maintaining posture in vertically inefficient architectures.
These results underscore that parallelism is not merely a mechanical curiosity—it provides concrete, testable benefits in real-world robot performance.
Conclusion
As the field moves toward more agile, resilient, and efficient humanoid robots, architectural decisions must be backed by quantitative reasoning. This work demonstrates that even subtle differences in kinematic layout can have significant consequences for manipulability, robustness, and overall system dynamics.
The use of constraint-based modeling, powered by modern libraries like Pinocchio, makes it possible to generalize and evaluate complex designs efficiently. The methodology developed here allows for performance-driven design that includes both serial and parallel mechanisms.
All CAD models and simulation tools developed for this study are available on GitLab to support future research and collaborative design efforts. The goal going forward is to push this methodology toward full kinematic and actuation co-optimization, ultimately leading to more principled and performant robot designs.
References
- Virgile Batto et al., “Comparative Metrics of Advanced Serial/Parallel Biped Design and Characterization of the Main Contemporary Architectures,” IEEE Humanoids 2023.
- Pinocchio Library. https://github.com/stack-of-tasks/pinocchio
- Kangaroo Robot: A. Roig et al., “Hardware Design of the Kangaroo Robot,” ICRA 2022.
- Talos Platform: O. Stasse et al., “TALOS: A New Humanoid Research Platform,” Humanoids 2017.
- Agility Robotics. Digit Robot Overview. https://www.agilityrobotics.com
- Wensing et al., “Proprioceptive Actuator Design in the MIT Cheetah,” IEEE T-RO 2017.
- GIM et al., “Disney Biped Robot Design,” IROS 2018.
- LIM et al., “WL and WABIAN Robots,” Philosophical Transactions of the Royal Society A, 2007.